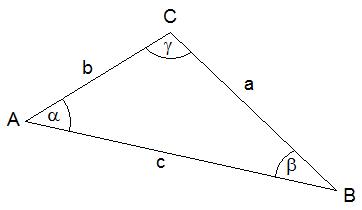
Benötigte Formeln:
sin(alpha)/a = sin(beta)/b = sin(gamma)/c
Hieraus folgt z.B.
a/b = sin(alpha)/sin(beta) oder auch a/sin(alpha) = b/sin(beta).
Verwendet wird außerdem die Winkelbeziehung
alpha + beta + gamma = 180°, um den noch fehlenden Winkel zu
berechnen, falls zwei Winkel bekannt sind.